harisrid Tech News

Background to the Problem

Hi all

Today, I’ll be sharing how to tackle a leetcode medium-level difficulty problem. Our problem under question is Leetcode 1911 : Maximum Alternating Subsequence Sum. It’s a classic dynamic-programming problem, where in an efficient solution leveraging linear memory is needed in order to obtain polynomial time performance.

The problem took me fifeteen minutes to solution and five minutes to debug. When I solve problems, I like to follow a templated structure. In this case, I first typed a line titled Approach & Categories; here, I categorized the problem in a Leetcode tag’s-esque style – Arrays, Recursion, and Dynamic Programming. This section framed and organized my mental thought process.

Next I went over complexity analysis. The first step involved defining my “alphabet soup” variables : N = length(input). I then solution-ed time complexity ( linear O(N) ) and space complexity : explicit O(N) array allocation and implicit O(1) constant single function call stack frame allocation .

I then followed up with a few notes on intuition and scenarios I wanted to cover. I wrote how the problem’s toughest aspect involved the handling of positive cases ( e.g. 4 – 2 + 5 – 3 ) or negative cases ( -4 + 2 – 5 + 3 ), depending on whether we did or did not select an element to start an alternating subsequence sum. The thinking of using two sums – one for even indices and another for odd indices – let to an allocation of the N*2 DP array.

The Solution’s Code

'''
1911. Maximum Alternating Subsequence Sum
URL := https://leetcode.com/problems/maximum-alternating-subsequence-sum/

Approach & Categories : Arrays, Recursion, Dynamic Programming

Complexity
N = len(input)
Time = O(N)
Space = O(N) ( Exp ) O(1) ( Imp ) 

Intuition :
- Have to handle for both positive cases and negative cases
- Think : if we select an element as starter, it's x + bestNegCase
- Else if no select, it's bestRunningPositiveCase
'''
class Solution:
    def maxAlternatingSum(self, nums: List[int]) -> int:
        mas = 0
        n = len(nums)
        dp = [[0 for i in range(n)] for j in range(2)]
        # base case = the first element
        posIdx = 0
        negIdx = 1
        dp[posIdx][-1] = nums[-1]
        dp[negIdx][-1] = -1 * nums[-1]
        bestPosSum = dp[posIdx][-1]
        bestNegSum = dp[negIdx][-1]
        mas = max(bestPosSum,bestNegSum)
        for idx in range(len(nums) - 2, -1, -1):
            startVal = nums[idx]
            # The bug was here! CAUGHT IT !!!!
curPosSum = max(startVal, startVal + bestNegSum)
curNegSum = max(-1*startVal, -1 * startVal + bestPosSum)
            bestPosSum = max(bestPosSum,curPosSum)
            bestNegSum = max(bestNegSum,curNegSum)
            dp[posIdx][idx] = bestPosSum
            dp[negIdx][idx] = bestNegSum
            # always start with positive element
            mas = max(mas,bestPosSum)
        return mas

Catching the Bug

Debugging this was somewhat tricky. I had to modify two lines so as to account for a case where the elements under selection themselves led to the best selection, versus the element + best running sum. Can you spot the subtle difference here?

Erroneous code :
curPosSum = startVal + bestNegSum
curNegSum = (-1 * startVal) + bestPosSum

Correct code :
curPosSum = max(startVal, startVal + bestNegSum)
curNegSum = max(-1*startVal, -1 * startVal + bestPosSum)

Performance Statistics

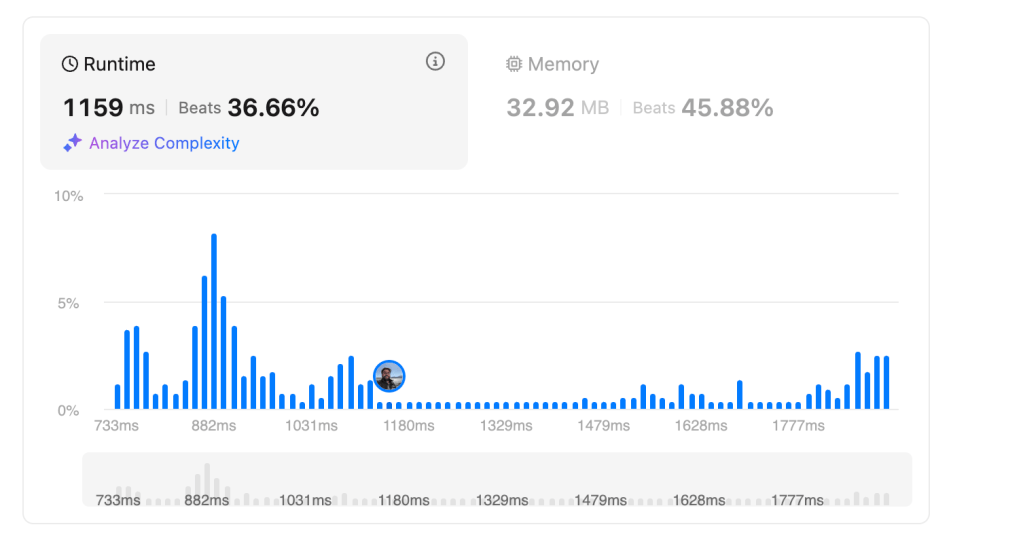
Now let’s see performance statistics too !